idiocy.org

Gaussian prime spirals

Gaussian integers are complex numbers where both the real and imaginary parts are integers. So \(3+7i\) is a Gaussian integer, but \(1/2+3i\) isn't.

Pretty straight-forward, right?

A Gaussian prime is, funnily enough, a Gaussian integer that is also a prime. Because complex numbers are a bit weird the rules for determining whether any Gaussian integer is prime are a little convoluted. Basically it boils down to:

Or:

A prime of the form \(4n+3\) simply means that if you subtract three and divide by four the resulting number should be an integer.

One thing to note about the Gaussian primes is that they are symmetrical around both the real and imaginary axes. This means that since \(13+8i\) is a prime, so are all \(±13±8i\). It’s also worth noting that all \(±8±13i\) are primes too. Lots of symmetry!

But what's this got to do with spirals, you ask. Well, nothing as far as I can see since they're not really spirals, but that seems to be the name that's stuck.

Start at \(8+13i\), which is a prime, and repeatedly add \(1\) until you reach another prime, \(10+13i\), then turn left, so now you’re adding \(i\) and continue until you reach another prime, \(10+17i\) and turn left again (\(-1\)) and continue repeating, you’ll eventually end up tracing over your previous path:

  1. \(8+13i\)
  2. \(10+13i\)
  3. \(10+17i\)
  4. \(8+17i\)
  5. \(8+13i\) (same as 1)
  6. \(10+13i\) (same as 2)
  7. etc.

It seems to be a rule that you will always end up tracing a loop, although it’s usually more complex than the square in the example above. For example \(-12-7i\) looks like this:

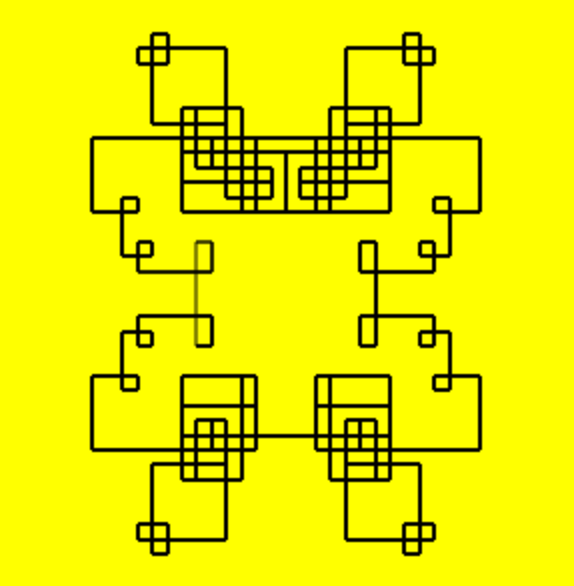
Screen-Shot-2014-09-21-at-10-38-14.png
Figure 1: \(-12-7i\) spiral

The “spirals” are quite attractive and nicely symmetrical. Or at least all the ones I’ve seen have been.

Screen-Shot-2014-09-21-at-10-44-09.png
Figure 2: \(5+5i\) spiral
 
+ \(i\)

Some numbers to try:

Note
The script above generates the spiral and displays it in the browser, but it can take quite a long time if the spiral is large, for example \(232+277i\). My intention was to include a corner count that updated as the spiral was generated so you could tell it was actually doing something, but battling the CSS on this page has put me off for the time being. I'll try and add it later.

For more information see:

t @flxzr
g alanthird
e Alan Third